빈도 (Frequency)
빈도란, 특정 범주에서 관찰된 사례의 수를 말한다. 좀 더 구체적으로, 30명으로 구성된 한 학급의 학생들의 행복 수준을 5점척도로 측정한다고 해보자. 이때 1점을 매긴 학생들이 2명, 2점을 매긴 학생들이 5명, 3점을 매긴 학생들이 10명, 4점을 매긴 학생들이 9명, 5점을 매긴 학생들이 4명이라고 하자. 이때 행복 수준이 1인 학생들의 빈도는 2, 행복 수준이 2인 학생들의 빈도는 5 ... (계속) 가 될 것이다.
빈도분포(frequency distribution): 빈도 분포는 각각의 범주에 사례수가 얼마나 있는지를 보여준다. 즉, 각각의 범주에 따라 빈도가 어떻게 퍼져있는지 보여주는 것이다. 이를 표로 나타낸 것을 빈도분포표라고 한다.
- 불연속 변인의 경우 각각의 범주에 따른 빈도 분포를 보여줌.
인종 빈도 백인 5 흑인 3 아시안 4 - 연속 변인의 경우 특정 값에 따른 빈도 분포를 보여줌.
- 연속변인의 경우, 만약 측정하는 수준이 너무 많다면 (예를 들면 10점 척도로 측정한 경우), 모든 점수에 따라 빈도를 각각 나타내는 것은 효율적이지 못하므로, 이러한 경우 백분위(percentile)을 사용하여 점수를 보여주는 것이 선호된다. 백분위(percentiles)란 특정 값보다 낮은 값의 사례수가 전체 집단 중 몇 %가 있는지를 나타내어 주는 표시 방법이다. 예를 들면, 100점 만점인 시험에서 50점이 17th percentile이라고 한다면, 50점보다 낮은 학생들이 전체의 17% 존재한다는 것을 의미한다.행복 수준 빈도 1 2 2 5 3 10 4 9 5 4
빈도 분포에는 여러 종류가 존재한다. 시각자료가 좋을 것 같아서 그려왔다.

대표값: 중심경향(central tendency)
중심경향이란 빈도에서 중심이 되는 값을 찾는 것을 말한다. 중심경향 측정치에는 우리가 잘 알고 있는 평균값을 포함해 최빈값, 중앙값 세가지가 존재한다.
최빈값(mode)
본포에서 가장 빈도가 높은 값으로 다음 행복수준을 예로 들었을 때 행복수준이 3일 때 빈도가 10으로 제일 높으므로 최빈값은 3이 된다. 일반적으로 최빈값은 질적연구에서 자주 사용되고, 양적연구에서는 잘 사용하지 않는다.
| 행복 수준 | 빈도 |
| 1 | 2 |
| 2 | 5 |
| 3 | 10 |
| 4 | 9 |
| 5 | 4 |
평균(mean)
평균이란 모든 점수의 합을 모든 점수의 개수로 나눈 것이라 할 수 있다. 아래는 통계치에 대한 평균을 나타내는 수식이다.
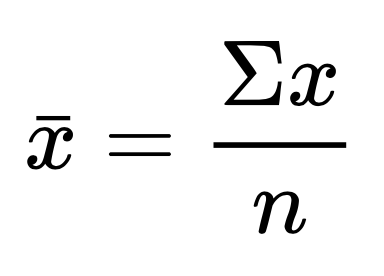
Ex. 특정 연구 점수가 10, 5, 9, 8, 6, 5, 9 일 때 평균? (10+5+9+8+6+5+9)/7을 계산한 값이 되겠다. 만약 분포가 단봉분포이고 완벽히 대칭적인 경우 평균과 최빈값은 같아지게 된다.
*평균은 통계학자들이 가장 선호하는 추정치로 다음과 같은 특징을 지닌다: Unbiased(큰 오차가 존재하지 않음), Efficient(효과적임), Consistent(일관적임)
*평균은 가장 자주 사용되고 가장 유용한 중심경향치이긴 하지만, 극단적인 값이나 비대칭분포에 의해 크게 영향받는 경향이 있다. 예를 들면 1,1,1,3,3,3,5,5,100의 값이 있다고 해보자. 이 값의 평균은 (1+1+1+3+3+3+5+5+100)/9로 대략 13.5점이 나오는데, 이상치인 100을 빼고는 나머지 값이 모두 1~5사이에 있으므로 좋은 중심이 되는 값이라 하기 어렵다.
중앙값(median)
중앙값이란 모든 점수가 낮은 값에서 큰 값으로 정렬되었을 때 중앙에 있는 점수를 말한다. 위 행복 수준을 예로 들어 낮은 값에서 큰 값으로 정렬해보면 다음과 같다: 1, 1, 2, 2, 2, 2, 2, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 4, 4, 4, 4, 4, 4, 4, 4, 4, 5, 5, 5, 5 여기서 중앙에 있는 값이 두 개이므로 두 값의 평균 (3+3)/2이 중앙값이 된다. 만약 빈도가 홀수값이라 중앙에 있는 값이 하나라면, 그 중앙에 있는 하나의 값이 중앙값이 된다. 중앙값은 50 percentile과 같은 값을 지닌다.
* 중앙값은 이상치(outlier; 혼자 극단적으로 다른 값을 지니는 값)가 있는 경우 좋은 대표값이 될 수 있다. 이 때 중앙값은 3으로 중심이 되는 값에 더 가깝다고 볼 수 있는 것이다. 그러나 중앙값은 추론통계에서는 거의 사용하지 않는다.
분산도(variability)
분산도란 점수 값들이 얼마나 다른 값과 차이가 있는지, 얼마나 점수 값들이 퍼져있는지, 얼마나 점수값이 평균값과 멀리 떨어져있는지 측정해주는 값이다. 분산도에는 범위, 분산, 표준편차의 세가지 측정치가 존재한다.
범위(Range)
가장 큰 값에서 가장 작은 값을 뺀 값으로 다음 행복수준 예시에서 보면 5-1 = 4 이므로 4가 범위가 된다. 쉽지만, 우리는 범위로부터 데이타에 대한 정보를 별로 얻지 못한다. 예를 들어 1,1,1,2,2,2,3,3,3,100의 데이타 셋의 경우 100-1=99로 99가 범주가 되지만 범위만으로는 데이타가 한쪽으로 몰려있는지 전혀 알 수 없다.
| 행복 수준 | 빈도 |
| 1 | 2 |
| 2 | 5 |
| 3 | 10 |
| 4 | 9 |
| 5 | 4 |
사분범위(Interquartile Range; IQR)
사분범위란 분포의 양 끝 1/4을 제외한 범위라고 할 수 있다. 위에서 살펴본 백분위(percentile)를 다시 살펴보면 이를 네등분 한 것이 사분위(interqurtile)이며, 제 1사분위수(Q1)는 25% 백분위수, 제 2사분위수(Q2)는 50% 백분위수 혹은 중앙값, 그리고 제3사분위수(Q3)는 75% 백분위수이다. 즉 사분범위란 75% 백분점수에서 25% 백분점수를 뺀 값이다.

분산(variance)
분산은 각각의 점수가 평균으로부터 떨어진 정도를 나타낸다. 따라서 아래 수식에서도 분산을 정할 때 각각의 점수와 평균의 차이를 통해 구하는 것을 볼 수 있다. 분산은 평균으로부터의 편차를 제곱한 것의 평균을 말한다. 여기서 편차는 평균과 점수의 차이를 지칭한다.
*왜 편차의 평균을 사용하지 않고 편차의 제곱의 평균을 사용할까? 그 이유는 점수와 평균의 차이값이 양수와 음수를 모두 가지기 때문에 편차를 모두 더할 경우 0이 되기 때문에 제곱하여 평균과 떨어진 정도를 측정하는 것이다.

예를 들어 다음과 같이 3점 척도에서 빈도를 구했다고 쳐보자. 이때의 평균값은 (1+1+2+2+2+3+3)/7=2가 될 것이다.
| 행복 수준 | 빈도 |
| 1 | 2 |
| 2 | 3 |
| 3 | 2 |
각 값을 평균으로 뺀 후 제곱한 것을 모두 더하여 평균을 내면 대략 0.57의 값이 나온다. 이를 분산이라고 한다.

표준편차(Standard deviation)
표준편차는 분산도를 알아보기위해 가장 많이 사용되는 수치로, 분산에 제곱근을 한 값이다.

위의 분산이 0.57로 나왔으니 이에 대한 제곱근은 0.75가 되고 이것이 표준편차값이다.

* 범위는 일반적으로 인구통계학적 정보(예: 연구참가자들의 연령 범위)를 보고할 때 사용되며, 이 외에는 딱히 유용하지 않다.
* 사분범위는 범위의 한계점을 보완해주며, 이상치에 덜 영향을 받는다.
* 분산과 표준편차는 추론통계에서 널리 사용되며, 극도로 유용하다.
모수치와 통계치의 표현
다시 저번 글에 이어 모수치와 통계치에 대한 이야기를 하고자 한다. 모수치는 모집단 데이타 수치를 지칭하고 통계치는 표본집단의 데이타 수치를 지칭한다고 했었다. 모수치와 통계치는 각각 다음과 같이 서로 다른 문자로 표현한다.

추론통계의 일반적 형태
t검정이든 ANOVA든 회귀든 모든 추론 통계는 일반적으로 다음과 같은 형태를 띈다.
(통계치-모수치)/분산도
Z 점수(Z score, 표준점수)
"Z score is the number of standard deviations that a raw score is above or below the mean"
Z 점수는 데이타에서 한 점수가 얼마나 평균으로부터 떨어져있는지를 알려주는 점수이다. 우리가 척도에서 바로 구한 점수는 모두 원점수(raw score)이다. 원점수(X)는 다음과 같은 식을 통하여 Z점수로 변환될 수 있다. Z 점수는 서로 다른 정규분포에서의 점수를 표준 점수로 변환시켜 비교할 수 있게 해주며, 정규분포 내의 해당 점수의 확률을 계산할 수 있게 해주는 등 아주 유용하지만, 논문 등에서 직접 Z점수가 나오는 경우는 많이 없다. 논문 등에서는 평균과 표준편차는 자주 보이지만 Z점수, 중앙값, 최빈값은 자주 나오지 않는다.
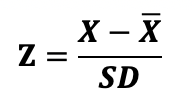
'Study > 통계 공부 + R' 카테고리의 다른 글
| 기초통계. 이변량 통계1: 상관분석 기초 (0) | 2020.12.03 |
|---|---|
| R 시작하기: csv 및 excel 데이타 불러오기 (4) | 2020.12.03 |
| 통계 프로그램 R 설치하기, R Studio 설치하기 (Mac 기준) (5) | 2020.12.03 |
| 기초통계. 기본 개념2 (표집오차, 신뢰도, 타당도) (0) | 2020.12.03 |
| 기초통계. 기본 개념1 (기술/추론 통계, 표집방식, 변인, 척도) (0) | 2020.12.02 |




댓글