구조방정식(Structural Equation Modeling; SEM)이란?
구조방정식은 많은 모델을 포함하는 일반적인 분석 틀이라고 할 수 있음. 다만 구조방정식은 다음과 같이 기존의 전통적인 모델로는 불가능했던 많은 중요한 확장을 가능하게 해줌.
- 다양한 종속 변수를 포함하는 모델
- 복잡한 매개 기제를 검증
- 측정 오류를 설명하기 위해 잠재 변수 추정
- 집단 간 모델의 불변성 검증
- 이분 / 서열 척도로 잠재요인 추정하기
- 반복측정치로 성장 궤도 모형 만들기
구조방정식의 장점 & 단점
장점
- 다양한 모수치의 구조 및 검증을 가능케 하여 크게 유동적임
- 기존의 방식으로는 단계적인 방식을 사용했어야했지만, 구조방정식은 많은 유형의 동시 검증을 가능케 함
- 정상적이지 않은, 불연속적 데이타를 측정할 수 있는 많은 대안적 방법론을 제공해줌
- 종단 데이타에 강력하고 엄격한 개별 안정성/변동성 검증을 제공해줌
단점
- 모델들이 이론에 기반하지 않고 점점 멀어질 수 있음
- 모델이 "적합(fit)"한지 결정하기 어려운 측면이 있음. 극단적으로 다른 모델이 똑같이 그 데이타에 적합하다는 결과가 나올 수 있음
- 철학적 사각지대: 구조방정식은 증거의 부재를 통해 가설을 지지함
- 안정적인 모델 추정을 위해 많은 피험자 수를 요구함. + 얼마나 많은 피험자 수가 충분한 것인지 애매함
- 구조방정식은 형편없는 표집이나 측정 과정에 대한 문제를 수정해주지 못함
행렬(matrix)
행렬이란?
- 구조방정식을 할 수 있는 많은 소프트웨어들은 행렬 대수학에 대한 기본 이해를 요함
- 행렬은 2차원적으로 나열된 수의 집합임
- 데이타 행렬은 n개의 행(row)과 p개의 열(column)을 가짐
- 스프레드시트에 정리된 데이타는 모두 행렬임
행렬의 특징
- 행렬은 주로 굵게 씌여진 대문자 알파벳 레터로 나타냄
- 행렬의 순서는 행과 열(r x c)로 이루어져있음. 예를 들어 다음 행렬은 2x4의 순서로 이루어짐

- 어떤 행렬에서 i 행과 j열은 Aij로 표시되며 여기서 i는 행, j는 열을 나타냄
- 두 행렬은 만약 순서가 같고 일치하는 요소들이 모두 같을때만 그 두 행렬이 같다고 할 수 있음
행렬들
- 한 행렬을 Transpose하면, 각각의 행과 열의 요소들을 상호변환하는 것인데, A(rxc)는 A'(cxr)이 된다고 할 수 있음
- 대칭적인 행렬(symmetric matrices)이란 행렬이 transpose한 행렬과 같은 경우를 말함: A = A' (공분산, 상관 행렬은 대칭적이라 할 수 있음)
- 사선 행렬(diagonal matrix)이란 대각선에 0이 아닌 값을 지니지만 그 외는 모두 0인 대칭적 행렬로 많은 잠재변수 모형들에서 잔차 공변량 행렬(residual covariance matrix)이 이에 속함
- 벡터(vector): 한 열을 가지는 행렬
공분산 행렬 (covariance matrix)

위 이미지를 보고 우리는 무엇을 알 수 있나?
- 변수가 3개임
- 각 변수의 분산을 알 수 있음 (covariance of itself is variance), 그리고 여기서 루트를 씌워주면 우리는 각각 변수의 표준편차도 알 수 있음.
- 변수 간 관계를 알 수 있지만 상관처럼 표준화된 값이 아니기에 관계의 강도(strength)를 알 수 없음
- 오직 양적/부적 관계인지만을 알 수 있음
공분산 & 상관 행렬


위 이미지를 보고 무엇을 알 수 있나?
- 이제는 관계의 강도 알 수 있음; x와 z의 관계의 강도는 x와 y의 관계보다 강함
공분산 & 상관 행렬 & 평균


위 이미지를 보고 무엇을 알 수 있나?
- 평균, 분산(표준편차), 상관에 대한 정보가 있음
- 따라서 우리는 이 정보를 통해 회귀 모형을 알 수 있음. 왜냐면 궁극적으로 회귀는 공분산이기 때문
- y=b0+b1*x
- y=b0+b1*z
- y=b0 +b1*x+b2*z
다중회귀(Multiple Regression) 리뷰
- 다중회귀(중다회귀)는 여러 독립(예측)변수를 하나의 종속(결과)변수에 회귀하는 것
- 일반적으로 종속변수는 연속변수이며, 표준분포를 보이며, 독립변수는 여러 형식을 띌 수 있음
- 모든 예측 변수를 함께 검증하는 joint 검증이 존재함(omnibus F-test, multiple R-squared)
- 다른 예측 변수를 넘어 하나의 개별 예측변수만을 독립적으로 검증할 수도 있음(raw & standardized betas, squared semi-partial correlations)
- 모델 요소: y=b0 +b1*x1+b2*x2 +e
- 여기서 잔차(e)는 결과변수에 대한 관찰된 값과 예측된 변수의 차이임
- 추정은 잔차의 제곱의 합을 최소화하는 모수치값을 선택하는 것에 집중함
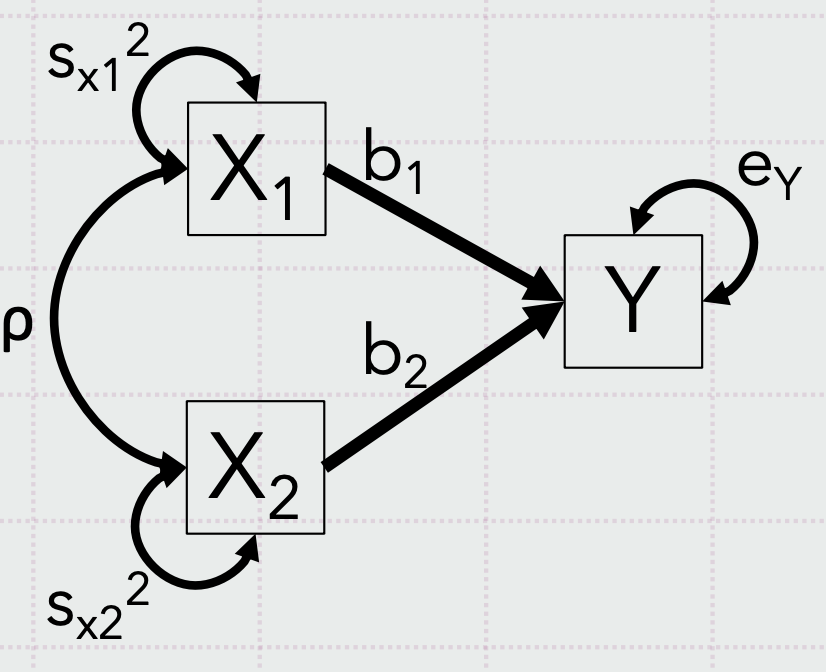
SEM 경로 모형
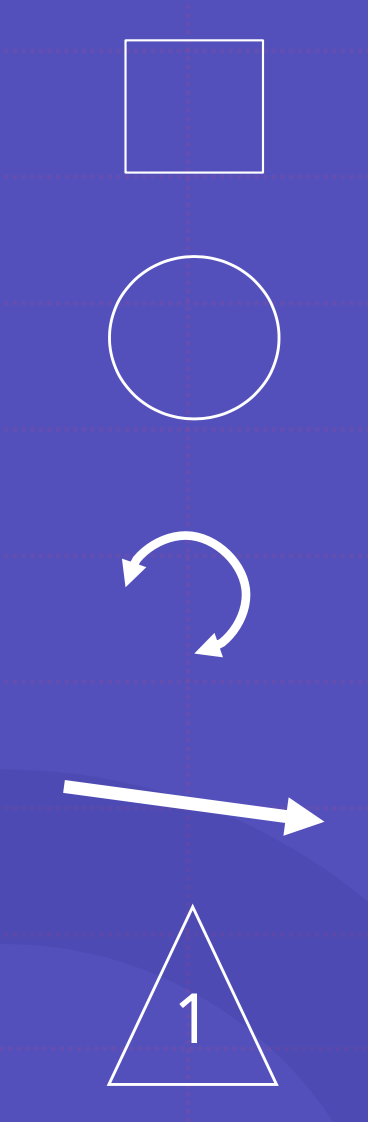
1. 네모 박스는 관찰변수, 지표변수를 나타냄
2. 원은 잠재(비관찰변수)변수를 나타냄
3. 양방향 화살표는 공분산을 나타냄
4. 일방향 화살표는 회귀를 나타내며, 예측변수에서 결과 변수로 향함
5. 세모는 상수를 나타냄. 여기서는 1의 경우를 보여줌
경로모형 exercise
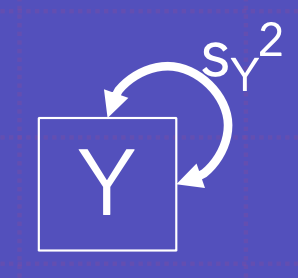
Y에 대한 분산을 나타냄
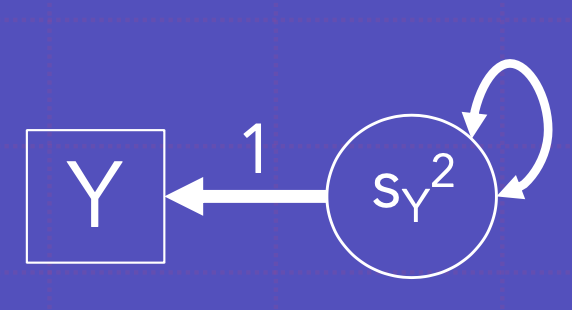
이 역시 Y에 대한 분산을 나타냄; 왜냐면 Y에 대한 분산 전체를 잠재변수 Y로 회귀하기 때문
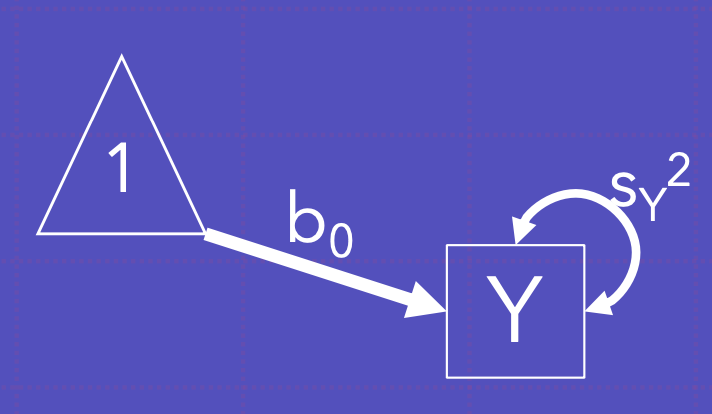
Y의 평균을 나타냄; Y의 분산을 알고, 1을 통해 Y에 회귀하기 때문에 평균을 얻을 수 있음.
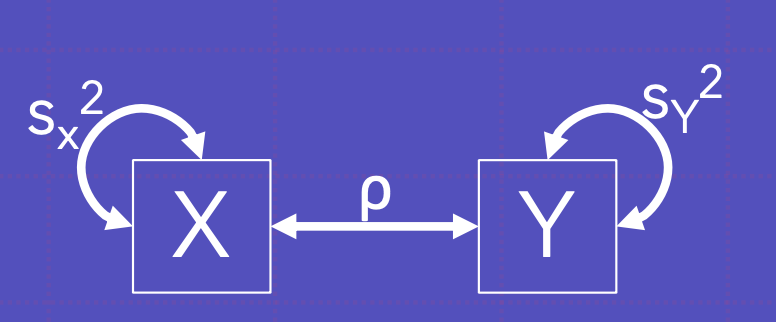
이게 실제 경로모형이라 할 수 있음. Y와 X 모두 관찰 변수이며 각각 공분산이 있으며, 둘은 상관관계에있음. 여기서 평균은 모름.
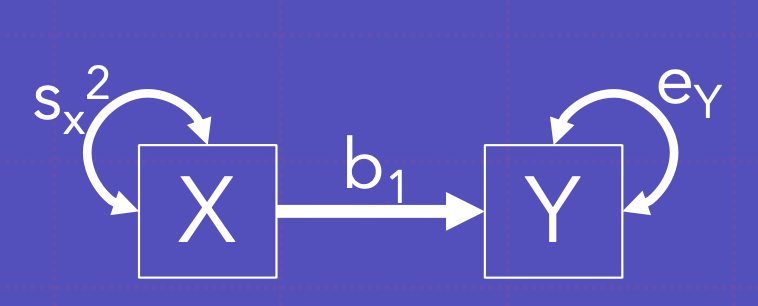
이는 회귀이고, X가 예측, Y가 결과변수임. 공분산과 차이 없게 두 변수간의 관계를 알려주지만, 회귀를 사용하는 경우, 이론적 바탕을 통해 X가 예측변수임을 가정했거나 등 했을 경우임

일반적인 다중 회귀 모형. 두 예측변수가 하나의 결과 변수를 예측해주고, 예측변수 간 상관관계가 있음을 볼 수 있음
Lavaan Syntax
~~ 공분산; y~~y 는 y의 공분산을 나타냄
~ 회귀: y~x는 y가 x에 회귀함을 나타냄
~1은 평균 추정을 나타냄; y~1은 추정된 y의 상수항을 나타냄
+ 는 단일 연산에서의 여러 변수를 나타냄; y~x+y는 y가 x와 y에 회귀함을 나타냄
=~ 는 잠재변수의 추정치를 나타냄; lv=~x+y 는 잠재변수 lv가 x와 y에 의해 추정됨을 나타냄
Syntax Practice
• Imagine that you have a dataset of subjective pleasure ratings (1-10) from participants who listened to following genres:
- Rock
- Pop
- Jazz
- Folk
- You also have these participants’ rating of their mood
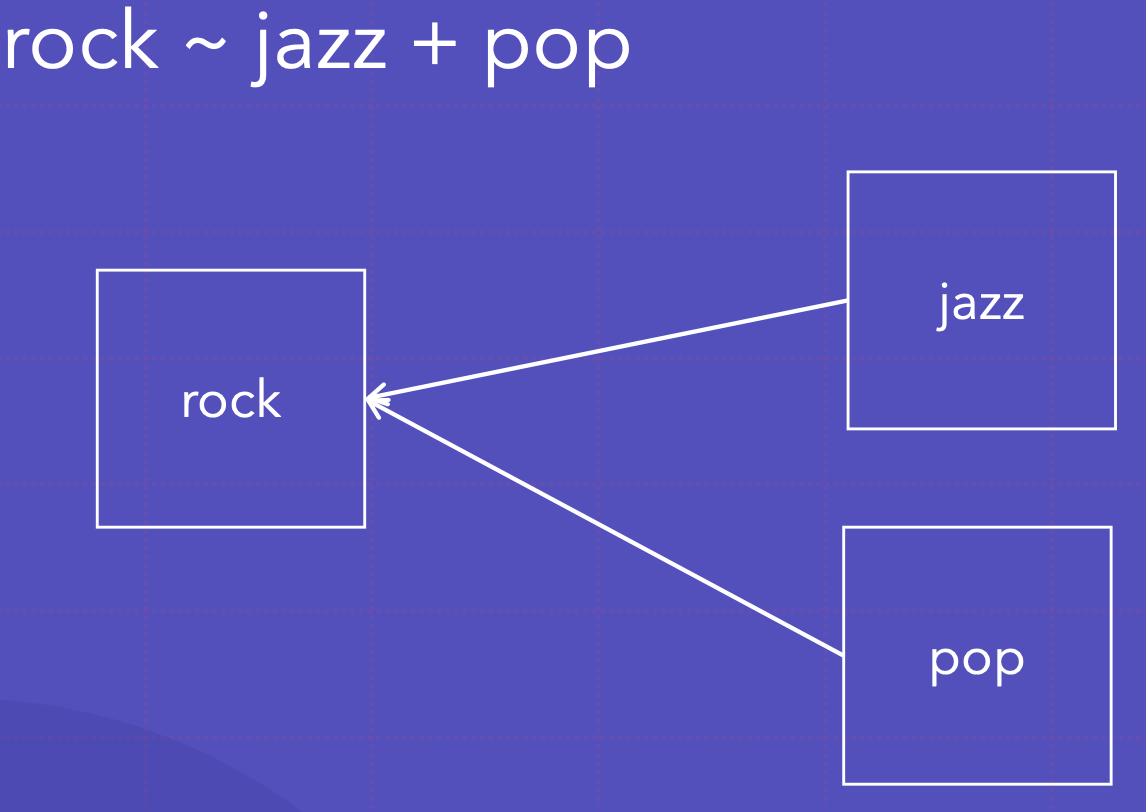
재즈&락 공분산
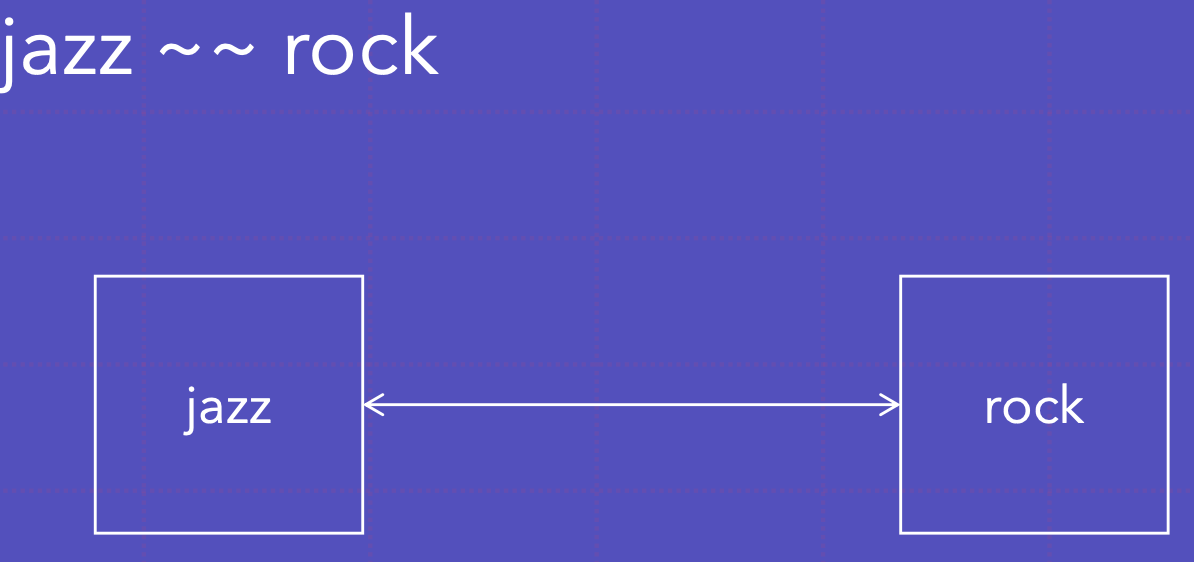
폭의 분산
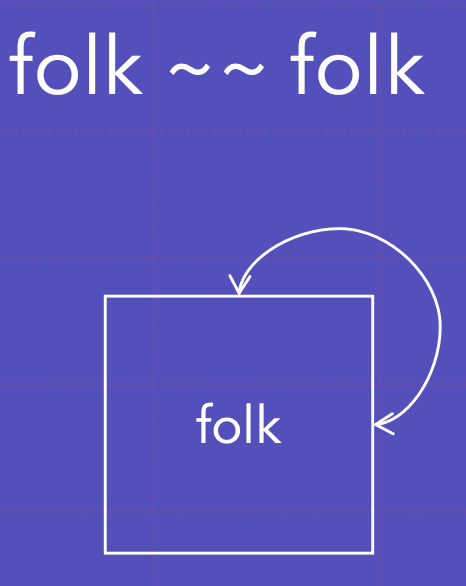
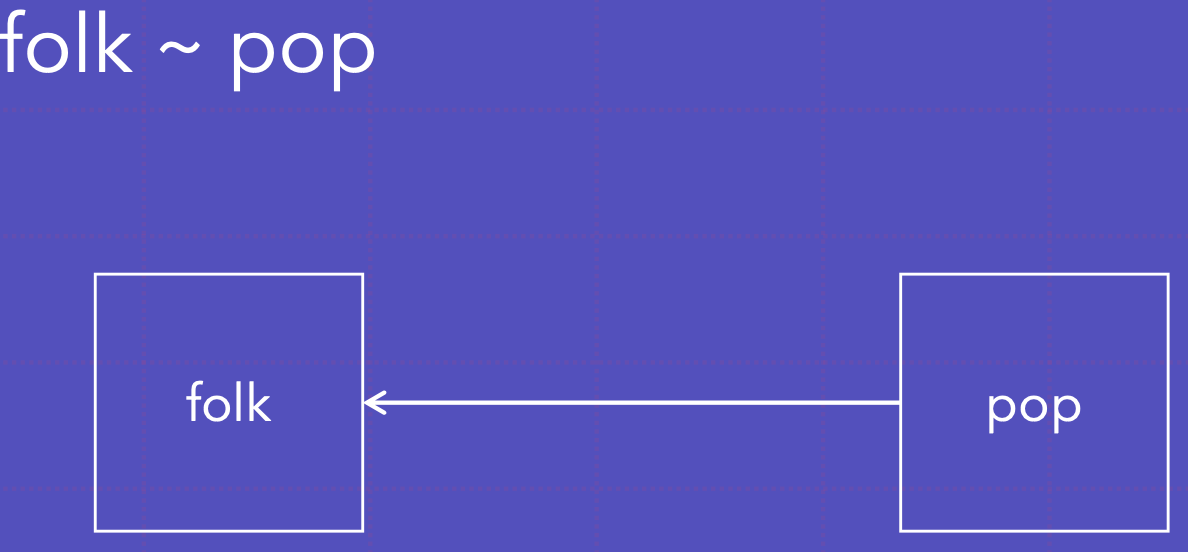
폭이 팝이 회귀함
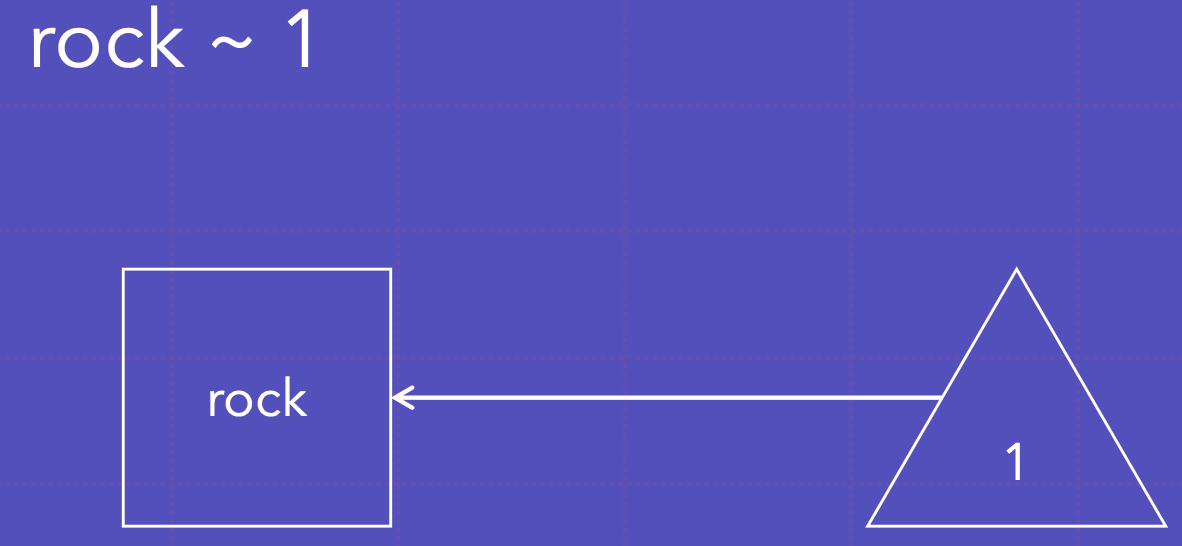
록에 대한 평균
재즈와 팝이 록에 회귀함
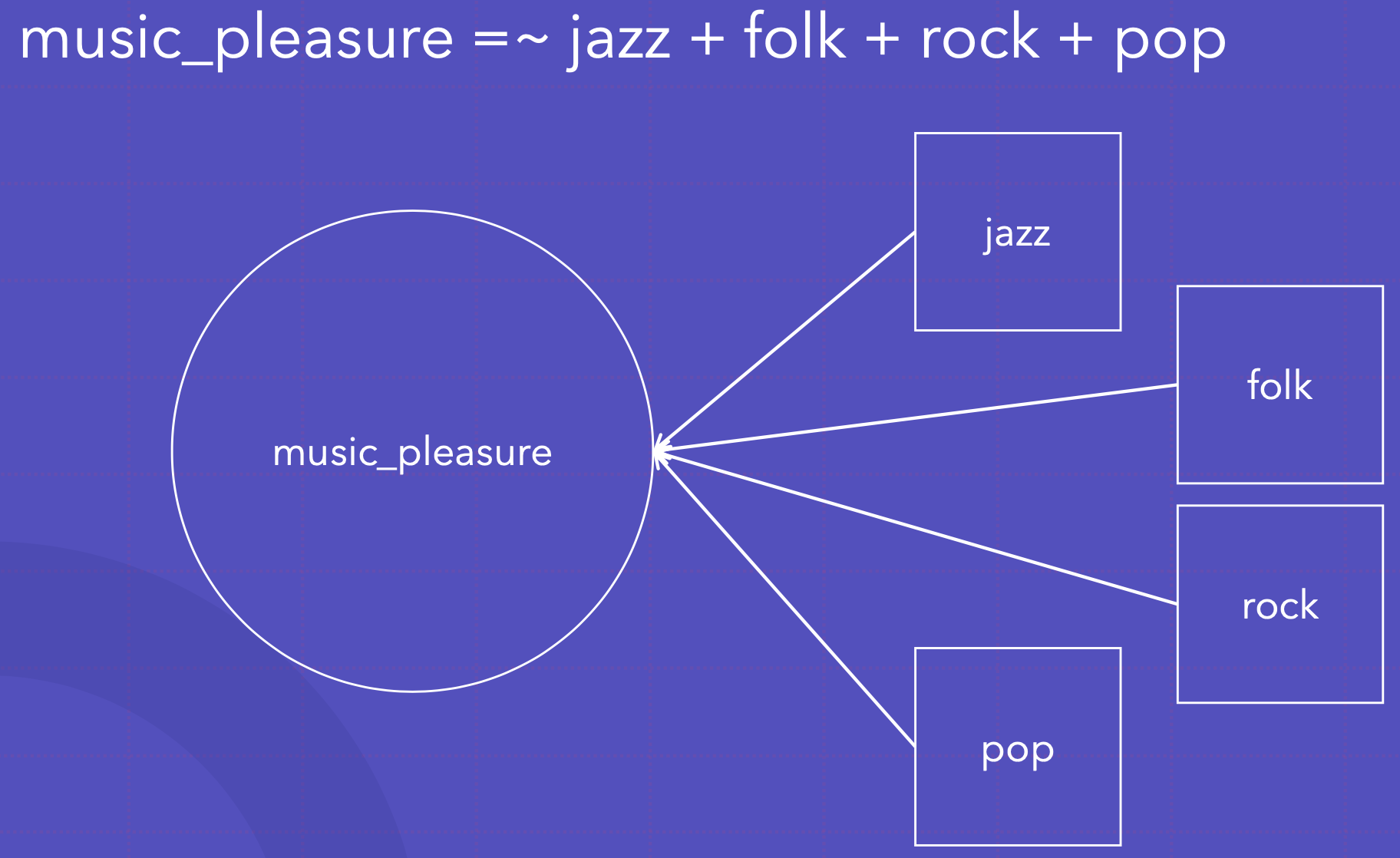
뮤직플레져가 재즈, 퐄,락,팝에 의해 측정됨
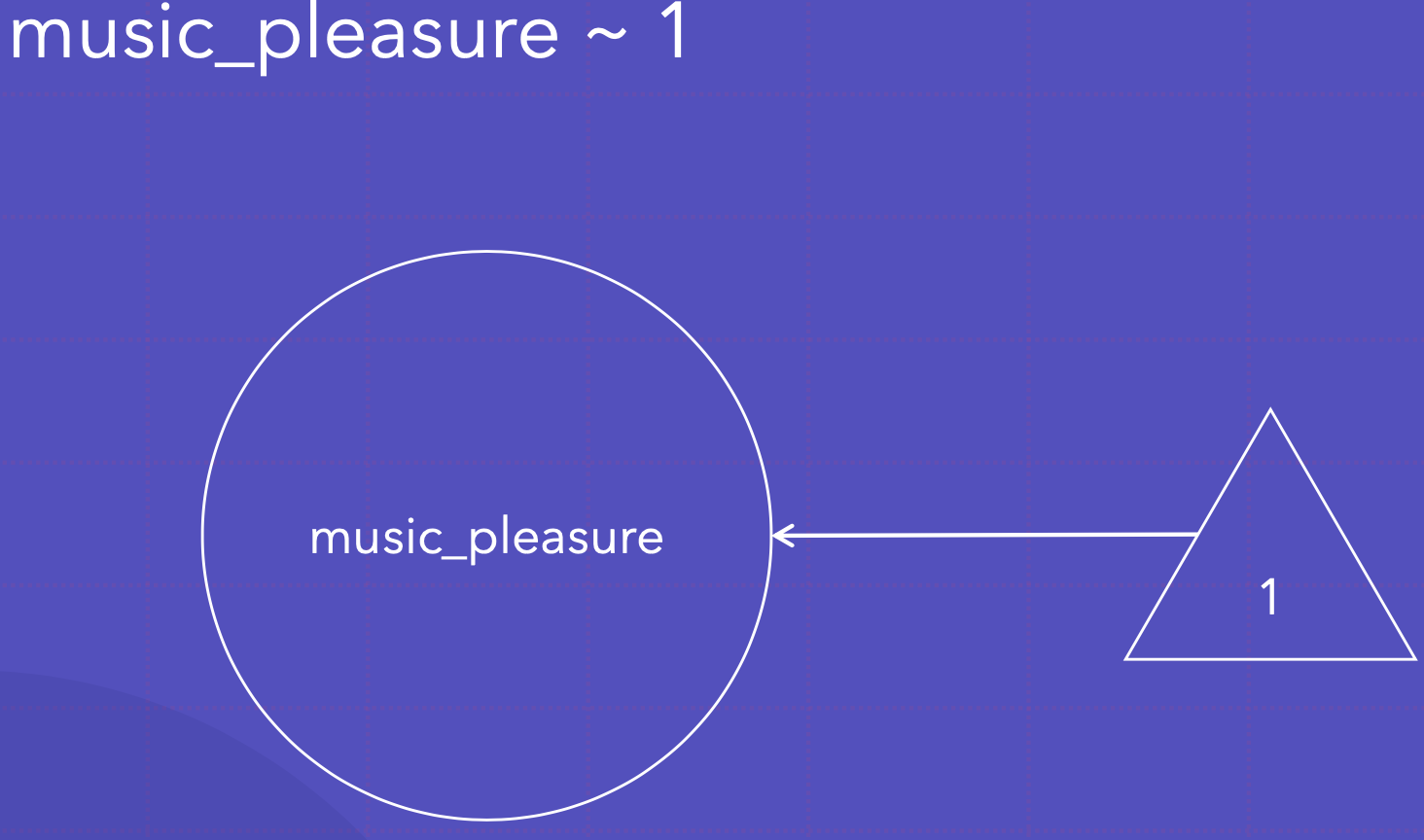
뮤직플레져의 상수항
|
mod1 <- ‘
music_pleasure =~
jazz + folk + rock + pop
mood ~ music pleasure
’
fit1<- sem(mod1, data =d) |
|||||||
|
• Defining a model between the marks :
‘ y~x' |
|||||||
|
• A generic model call: sem
|
|||||||
'Study > 통계 공부 + R' 카테고리의 다른 글
| SEM 책 정리 (1)구조방정식 소개 (0) | 2022.01.28 |
|---|---|
| SEM 구조방정식 (2) (0) | 2022.01.28 |
| 범주화하기: 로지스틱 회귀, r 통계 분석 (0) | 2021.01.01 |
| 기초통계: 가설 검정 (0) | 2020.12.21 |
| 기초통계: 표준점수 (Z점수; Z score) (0) | 2020.12.18 |



댓글