300x250
SEM 고려사항
SEM 모델은 두 개의 자유도(df)를 지님
- 하나는 표본 크기(sample size; N)과 관련 있으며, 표준오차(SE)의 추정 및 모수 추정치의 유의도 평가에 중요한 역할을 함.
- 또 다른 하나는 데이타의 평균 및 공분산으로부터 얼마나 많은 정보를 가지고 있는지와 관련있음.
자유도(degrees of freedom)란?
- 공분산 행렬을 다시 보자.

- 3개의 공분산과 3개의 분산이 있음 = 총 6개의 정보들이 존재함
- 3개의 평균 = 3개의 평균에 대한 정보가 있음
- 모든 모델 적합도는 위 정보에 의해 제한됨. 즉 우리는 3개의 분산이나 3개의 공분산, 혹은 3개의 평균 이상을 요구하는 모형을 추정할 수 없음
- 우리가 더 많은 정보를 요구하는 모형 적합도를 구하려한다면? 그 모델은 "over-identified"될것임; 데이타가 충분치 않음!
과포화 & 저포화 모형 (over- and under-identified model)
- 과포화모형: 데이타가 제공하는 것보다 더 많은 추정치를 요구하는 경우
- 포화모형(identified model; saturated model): 가지고 있는 모든 모수에 대해 추정을 요구하는 경우 (e.g., 일반적인 회귀 모형)
- 제한이나 가정이 없음
- 모델 적합도를 평가하는 데 유용하지 않음. 데이타에 완벽하게 적합한 모형임
- 저포화모형: 포화모형과 비교했을 때 이론적 혹은 통계적으로 모델 적합도를 평가할 수 있도록 제한을 가짐.
모델적합도(Model Fit)
- SEM은 모델 적합도를 평가하기에, SEM 결과는 디폴트로 모델 적합도 통계치를 보고해줌.
- 카이스퀘어(Ch Square): 예측된 모형과 관찰된 모형이 같다는 영가설을 검증함; 유의미하지 않은 카이스퀘어 결과의 경우(p >. 05) 성공적인 모델을 가지고 있음을 의미함!
- 하지만 카이스퀘어는 표본 크기에 아주 민감하기 때문에 크게 유용하지 않음. 대체적으로 유의미하게 나옴
- 일부 학자들은 카이스퀘어 통계치 그 자체를 모델 적합도 측정치로 사용하는 것을 추천하기도 함; 일반적 기준점: (X^2/df)<=5
모델적합도(Model Fit): 더 나은 선택지들
- 모델 적합도에 대한 다른 모든 측정치는 하나의 값으로 구성되어있으며, 통계학자들이 정한 기준점과 비교하여야 함
- 예를 들어 CFI(Comparative fit index)에 대한 일반적인 기준점은 .90임
- 문제점은 이러한 기준점이 완전히 동의된 지표는 아니라는 것이다. 예를 들면 일부 학자들은 .90을 기준점으로 제시하지만, 다른 학자들은 더 보수적으로 .95를 제안하기도 함.
잠재변수이론(Latent Variable Theory)
잠재변수의 유형
- 잠재 계층(Latent Class): 계층화 혹은 집단 변수 (e.g., 서로 다른 학습 장애를 가진 학생들)
- 연속적 잠재 변수: (e.g., IQ)
- 지표들은 연속적이거나 불연속적일 수 있으며, 이는 잠재 변수의 유형을 나타내는 것은 아님.
- 예시: SES(사회경제적 지위)
- 사회경제적 지위를 측정하는 많은 방법이 있음; 교육 수준, 소득수준, 부모의 소득 수준 등등
- 이러한 지표들은 함께 변하지 않지만, 잠재 변수(SES)는 연속적으로 일관적으로 변화한다고 가정함
- 만약 이러한 가정이 말이 되지 않는 경우 잠재 계층을 사용할 수 있음. 어떤 이론을 사용하는지가 어떤 것을 사용할 지 결정하는 데 핵심적으로 작용함
측정치 이론(Measurement Theory)
- 측정치 이론은 관찰치가 다양한 요소의 기능이라고 가정함: Xi = Ti + ei
- Xi는 관찰치임
- Ti는 측정된 대상의 진점수(true score)임
- ei는 잔차의 변산성으로 일반적으로 랜덤 잔차와 특정 원인 변수의 결합이라고 생각됨. ~N(0, σ2)
- 예를 들어 행복감을 여가시간, 햇빛, 친구관계로 측정한다고 해보자.
- 이 행복감은 몇 가지 요인들에 의해 교란(confounded)된다. 즉 이 행복감의 측정치는 일부 다른 요인에 의해 영향을 받는다.
- 진짜 오류
- 다른 식별되지 않은 원인으로부터의 특정 분산
- 따라서 각 문항들은 타겟 능력이나 타겟 속성보다 다른 요인에 대해 더 많이 얘기해 줄 것임
- 우리가 원하는 것은 우리가 원하는 그 속성의 진점수를 대표하는 측정치의 구성 요소를 추출/고립시키는 방식임
- xi = Ti + ei
- xi - ei = Ti
- 하지만 어떠한 관찰치에서도 ei가 무엇인지는 알 수 없음.
- 이 행복감은 몇 가지 요인들에 의해 교란(confounded)된다. 즉 이 행복감의 측정치는 일부 다른 요인에 의해 영향을 받는다.
잠재 변수 이론(Latent Variable Theory)

- 위 모델에서 우리는 각각의 수집된 측정치에서, 특정 그리고 랜덤 에러 변산성을 나누고 있음.
- 이는 지표들간 공통된 분산에 대한 정보를 사용하고 공통 요인을 가짐을 추론함으로 성취될 수 있음.


잠재 변수란 그렇다면 무엇일까? 모델의 관점에서 보면, 잠재 구성개념을 추론하기 위해 사용된 여러 측정치 간의 공통 분산일 뿐임.
공분산/상관

- 우리는 이 모델을 사용해 지표 변수들의 공분산을 추정할 수 있음
- Wright의 경로 다이아그램 추적 규칙을 사용할 수 있음
- 기온과 아이스크림 간의 공분산 구하기: 공통 분산에서 기온까지의 회귀 경로와 공통분산을 통해 이어지는 아이스크림까지의 회귀 경로: 1*9*.8 = 7.2
- 기온과 익사 간의 공분산 구하기: 1*9*.40 =. .6
- 아이스크림과 익사 간의 공분산 구하기: .8*9*.4= 2.88
- 기온의 분산 구하기: 1*9*1 + 25 =. 4
- 아이스크림의 분산: .8 * 9 * .8 + 16 =. 1.76
- 익사의 분산: .4 * 9 * .4 +9 =. 0.44
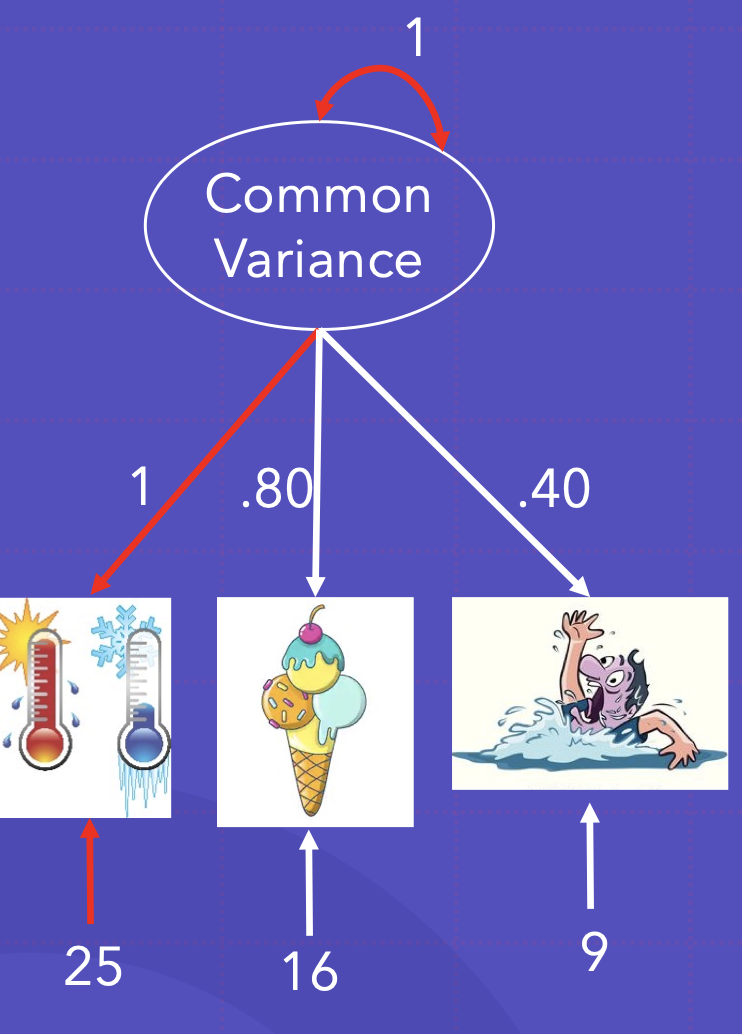
만약에 표준화된 요인 부하 대신 표준화된 요인을 원한다면 어떻게 될까?
- 만약 잠재 요인의 분산이 바뀐다면, 다른 요인 부하량 역시 바뀔 것임 e.g., 1*1*1 + 25 = 34가 아님
- 공분산은 바뀌지 않지만, 관찰된 데이타를 대표하기위해서 모형은 꼭 바뀌어야 함.
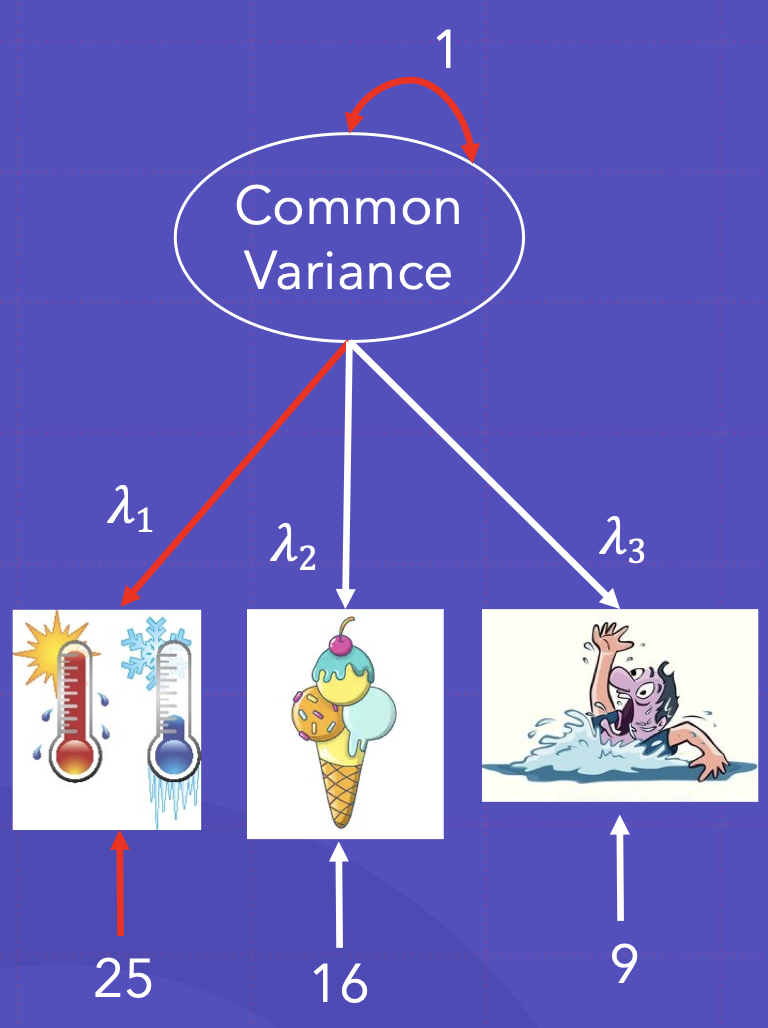
기온의 부하량:
- λ1 * 1 * λ1 + 25 = 34
- λ1^2 = 9
- λ1 = 3
아이스크림의 부하량?
- λ2 * 1 * λ2 + 16 = 21.76
- λ2^2 =. .76
- λ2 = 2.4
반응형
'Study > 통계 공부 + R' 카테고리의 다른 글
| SEM 책 정리 (2)데이타 정리하기 (0) | 2022.02.04 |
|---|---|
| SEM 책 정리 (1)구조방정식 소개 (0) | 2022.01.28 |
| SEM 구조방정식 (1) (0) | 2022.01.21 |
| 범주화하기: 로지스틱 회귀, r 통계 분석 (0) | 2021.01.01 |
| 기초통계: 가설 검정 (0) | 2020.12.21 |


댓글